
Understanding the Euclidean Algorithm for Finding GCD
What is GCD
What is GCD (Greatest Common Divisor): The Greatest Common Divisor, or GCD, is a fundamental concept in number theory, representing the largest positive integer that divides two numbers without leaving a remainder.
Euclidean Algorithm
What is the Euclidean Algorithm: Named after the ancient Greek mathematician Euclid, the Euclidean algorithm is a straightforward and efficient method for finding the GCD of two integers. It involves iteratively dividing the larger number by the smaller one until the remainder becomes zero.
Example: Let's use the Euclidean algorithm to find the GCD of 48 and 18.
Divide 48 by 18, resulting in a quotient of 2 and a remainder of 12.
- GCD(48, 18) = GCD(18, 12)
Divide 18 by 12, resulting in a quotient of 1 and a remainder of 6.
- GCD(18, 12) = GCD(12, 6)
Continue the process, dividing 12 by 6, resulting in a quotient of 2 and a remainder of 0.
- GCD(12, 6) = GCD(6, 0)
Since the remainder is now 0, the GCD is the last non-zero remainder, which is 6.
Explore the simplicity and effectiveness of the Euclidean algorithm in finding the Greatest Common Divisor of any two integers.
Code in cpp
int calcGCD(int n, int m){
while(n>0&&m>0){
if(n>m) n = n % m;
else m = m % n;
}
if(n==0) return m;
else return n;
}
Quick look
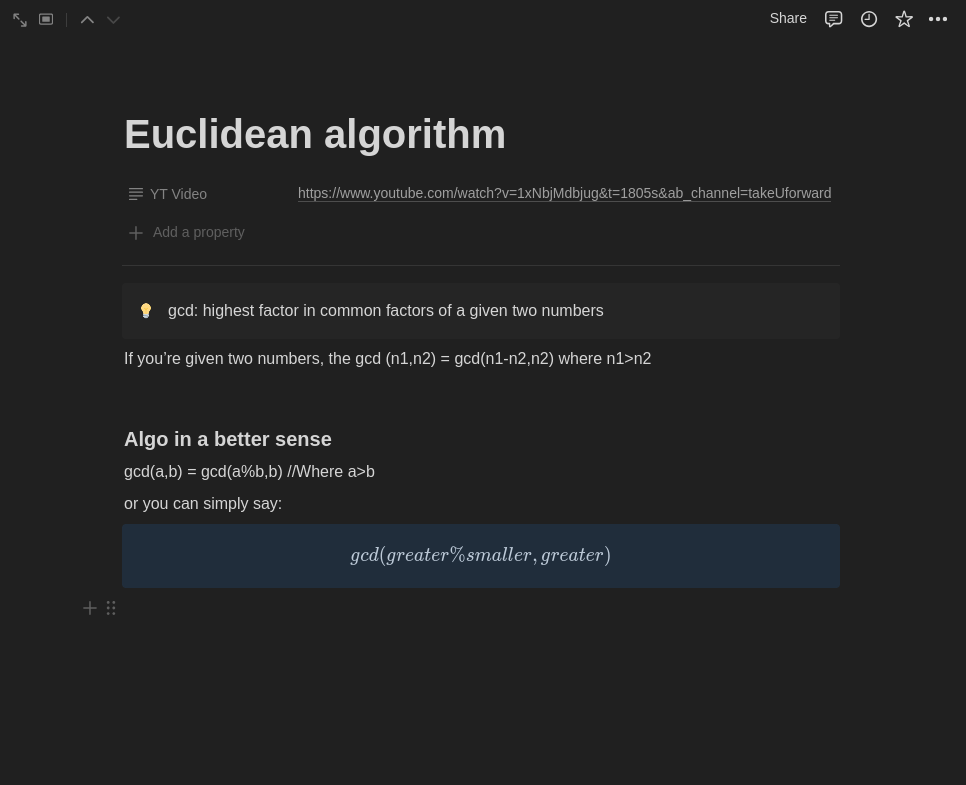
Video explanation: https://www.youtube.com/watch?v=1xNbjMdbjug&t=1805s&ab_channel=takeUforward
### What is GCD
What is GCD (Greatest Common Divisor): The Greatest Common Divisor, or GCD, is a fundamental concept in number theory, representing the largest positive integer that divides two numbers without leaving a remainder.
### Euclidean Algorithm
What is the Euclidean Algorithm: Named after the ancient Greek mathematician Euclid, the Euclidean algorithm is a straightforward and efficient method for finding the GCD of two integers. It involves iteratively dividing the larger number by the smaller one until the remainder becomes zero.
Example: Let's use the Euclidean algorithm to find the GCD of 48 and 18.
1. Divide 48 by 18, resulting in a quotient of 2 and a remainder of 12.
* GCD(48, 18) = GCD(18, 12)
2. Divide 18 by 12, resulting in a quotient of 1 and a remainder of 6.
* GCD(18, 12) = GCD(12, 6)
3. Continue the process, dividing 12 by 6, resulting in a quotient of 2 and a remainder of 0.
* GCD(12, 6) = GCD(6, 0)
4. Since the remainder is now 0, the GCD is the last non-zero remainder, which is 6.
Explore the simplicity and effectiveness of the Euclidean algorithm in finding the Greatest Common Divisor of any two integers.
### Code in cpp
```cpp
int calcGCD(int n, int m){
while(n>0&&m>0){
if(n>m) n = n % m;
else m = m % n;
}
if(n==0) return m;
else return n;
}
```
### Quick look

**Video explanation**: [https://www.youtube.com/watch?v=1xNbjMdbjug&t=1805s&ab\_channel=takeUforward](https://www.youtube.com/watch?v=1xNbjMdbjug&t=1805s&ab_channel=takeUforward)